Variety – part 1
Blog: Strategic Structures
The cybernetic concept of variety is enjoying some increase in usage. And that’s both in frequency and in number of different contexts. Even typing “Ross Ashby” in Google Trends supports that impression.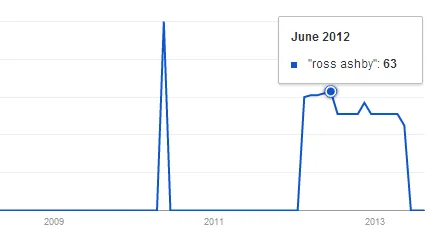
In the last two years the interest seems stable, while in the previous six – non-existing, save for the lonely peak in May 2010. That’s not a source of data to draw some conclusions from, but it supports the impression coming from tweets, blogs, articles, and books. On one side, that’s good news. I still find the usage insignificant, compared to what I believe it should be, given its potential and the tremendously increased supply of problems of such nature that if not in solving, at least it can help in understanding. Nevertheless, some stable attention is better that none at all. On the other side, it attracts a variety of interpretations and some of them might not be healthy for the application of the concept. That’s why I hope it’s worth exchanging more ideas about variety, and those having more variety themselves would either enjoy wider adoption or those using them – more benefits, or both.
The concept of “variety” as a measure of complexity had been preceded and inspired by the “information entropy” of Claude Shannon, also known as the “amount of surprise” in a message. That, although stimulated by the development of the communication technologies in the first half of the twentieth century, had its roots in statistical mechanics and Boltzmann’s definition of entropy. Boltzmann, unlike classical mechanics and thermodynamics, defined entropy as the number of possible microstates corresponding to the micro-state of a system. (These four words “possible”, “microstates”, “micro-states” and “system” deserve a lot of attention. Anyway, they’ll not get in this post.)
Variety is usually defined as the number of possible states in a system. It is also applied to a set of elements, as the number of different members determine the variety of a set, and to the members themselves which can be in different states and then the set of possible transitions has certain variety. This is the first important property of “variety”. It’s recursive. I’ll come back to this later. Now, to clarify what is meant by “state”:
By a state of a system is meant any well-defined condition or property that can be recognised if it occurs again.
Ross Ashby
Variety can sometimes be easy to count. For example, after opening the game in chess with pawn on D4, the queen has variety of three – not to move or move to one of the two possible squares. If only the temporary variety gain is counted, then choosing D2 as the next move would give variety of 9, and D3 would give 16. That’s not enough to tell if the move is good or bad, especially having in mind that some of that gained variety is not effective. However, in case of uncertainty, in games and elsewhere, moving to a place which both increases our future options and decreases those of the opponent, seems a good advice.
Variety can be expressed as a number, as it was done in the chess example, but in many cases it’s more convenient to use the logarithm of that number. The common practice, maybe because of the first areas of application, is to use binary logarithms. When that is the case, variety can be expressed in bits. It is indeed more convenient to say the variety of a four-letter code using the English alphabet is 18.8 bits instead of 456 976. And then, when the logarithmic expression is used, combining varieties of elements is done just by adding instead of multiplying. This has additional benefits when plotting etc.
Variety is sometimes referred to and counted as permutations. That might be fine in some cases but as a rule it is not. To use the example with the 4-letter code, it has 358 800 permutations (26 factorial divided by 22 factorial), while the variety is 456 976 (26 to the power of 4).
Variety is relative. It is dependant on the observer. That’s obvious even from the word “recognised” in the definition of “state”. If, for example, there is a clock with two hands that are exactly the same or at least to the extent that an observer can’t make the difference, then, from the point of view of the observer, the clock will have much lower variety than a regular one. The observer will not be able to distinguish for example 12:30 and 6:03 as they will be seen as the same state of the clock.
This can be seen as another dependency. That of the capacity of the channel or the variety of the transducer. For example, it is estimated that regular humans can distinguish up to 10 million colours, while tetrachromats – at least ten times more. The variety of the transducer and the capacity of the channel should always be taken into account.
When working with variety, it is important to study the relevant constraints. If we throw a stone from the surface of Earth, certain constraints, including those we call “gravity” and the “resistance of the air”, would allow a much smaller range of possible states than if those constraints were not present. Ross Ashby made the following inference out of this: “every law of nature is a constraint”, “science looks for laws; it is therefore much concerned with looking for constraints”. (Which is interesting in view of the recent claim of Stuart Kauffman that “the very concept of a natural law is inadequate for much of the reality” and that we live in a lawless universe and should fundamentally rethink the role of science…)
There is this popular way of defining a system as something which is more than the sum of its parts. Let’s see this statement through the lenses of varieties and constraints. If we have two elements, A and B, and each can be in two possible states on their own but when linked to each other A can bring B to another, third state, and B can bring A to another state as well. In this case, the system AB has certainly more variety than the sum of A and B unbound. But if, when linking A and B they inhibit each other, allowing one state instead of two, then it is clearly the opposite. That motivates rephrasing the popular statement to “a system might have different variety than the combined variety of its parts”.
If that example with A and B is too abstract, imagine a canoe sprint kayak with two paddlers working in sync and then compare it with the similar setting but one of the paddlers rowing while the other holds her paddle in the water.
And now about the law of requisite variety. It’s stated as “only variety can destroy variety” by Ashby and as “variety absorbs variety” by Beer, and has other formulations such as “The larger the variety of actions available to control system, the larger the variety of perturbations it is able to compensate”. Basically, when the variety of the regulator is lower than the variety of the disturbance, that gives high variety of the outcome. A regulator can only achieve desired outcome variety, if its own variety is the same or higher than that of the disturbance. The recursive nature, mentioned earlier, can now be easily seen, if we look at the regulator as channel between the disturbance and the outcome or if we account for the variety of the channels at the level of recursion with which we started.
To really understand the profound significance of this law, it should be seen how it exerts itself in various situations, which we wouldn’t normally describe with words such as “regulator”, “perturbations” and “variety”.
In the chess example, the power of each piece is a function of its variety which is the one given by the rules reduced by the constraints at every move. Was there a need to know about requisite variety to design this game? Or any other game for that matter? Or was that necessary to know how to wage war. Certainly not. And yet, it’s all there:
It is the rule in war, if our forces are ten to the enemy’s one, to surround him; if five to one, to attack him; if twice as numerous, to divide our army into two.
Sun Tzu, The Art of War
But let’s leave the games for a moment and remember the relative nature of variety. The light signals in ships should comply with the International Regulations for Preventing Collisions at Sea (IRPCS). Yes, here we even have the word “regulation”. Having the purpose in mind, to prevent collision, the signals have reduced variety to communicate the states of the ships but enough to ensure the required control. For example, if an observer sees one green light, she knows that another ship is passing from left to right, and – from right to left – if she sees red light. There are lots of states – different angels of the course of the other ship – that are reduced into these two but that is serving the purpose well enough. Now, if she sees both red and green that means that the ship is coming exactly towards her that’s an especially dangerous situation. That’s why the reduction of variety in this case has to be very low.
The relativity of variety is not only related to the observer’s “powers of discrimination”, or those of the purpose of regulation. It could be dependant also on the situation, on the context. An example that first comes to mind is the Easop’s fable “The Fox and the Stork”.
Fables, and stories in general, are interesting phenomenon. Their capability to influence people and survive many centuries is amazing. But why is that? Why do you need a story, instead of getting directly the moral of the story. Yes, it’s more interesting, there is this uncertainty element and all that. But there is something more. Stories are ambiguous, interpretable. They leave many things to be completed by the readers and listeners. And yes, to put in different words, they have much higher variety than morals and values.
That’s it for this part. Stay tuned.
Leave a Comment
You must be logged in to post a comment.
