From Distinction to Value and Back
Blog: Strategic Structures
I tried to explain earlier how distinction brings forth meaning, and then value. Starting from distinction may seem arbitrary. Well, it is. And while it is, it is not. That wouldn’t be very difficult to show, but until then, let’s first take a closer look at distinction. As the bigger part of that work is done already by George Spencer-Brown, I’ll first recall the basics of his calculus of indications, most likely augmented here and there. Then I’ll quickly review some of the resonances. Last, I’ll come back to the idea of re-entry and apply it to the emergence of values.
Recalling
If I have to summarise the calculus of indications, it would come down to these three statements:
To re-call is to call.
To re-cross is not to cross.
To re-enter is to oscillate.
In the original text, the “Laws of Form”, only the first two are treated as basic, and the third one is coming as their consequence. Later on, I’ll try to show that the third one depends on the first two, just as the first two depend on the third one.
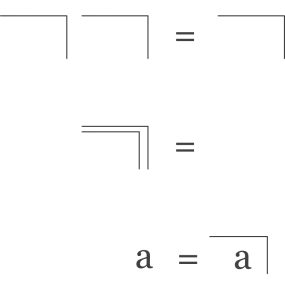
The calculus of indications starts with the first distinction, as “we cannot make an indication without drawing a distinction”. George Spencer-Brown introduces a very elegant sign to indicate the distinction:
It can be seen as a shorthand of a rectangle, separating inside from outside. The sign is called “mark” as it marks the distinction. The inside is called the “unmarked state” and the outside is the “marked state”. The mark is also the name of the marked state.
This tiny symbol has the power to indicate several things at once:
- The inside (emptiness, void, nothing, the unmarked state)
- The outside (something, the marked state)
- The distinction as a sign (indication)
- The distinction as on operation of making a distinction
- The observer, the one that makes the distinction
That’s not even the full list as we’ll see later on.
Armed with this notation, we can express the three statements:
They can be written in a more common way using brackets:
()() = ()
(()) = .
a = (a)
The sign “=” may seem as something we should take for given, but it’s not. It means “can be confused with”, or in other words: “there is no distinction between the value on the left side of the equation and the value on the right side”. Again, a form made out of distinction.
The first statement is called the law of calling. Here’s how it is originally formulated in the “Laws of Form”:
The value of a call made again is the value of the call.
If we see the left sign as indicating a distinction, and the right sign as the name of the distinction, then the right sign indicates something which is already indicated by the left sign.
Or let’s try a less precise but easier way to imagine it. If you are trying to highlight a word in a sentence and you do that by underlining it, no matter how much times you would draw a line below that word, at the end the word will be as distinguished as it was after the first line. Or if you first underline it, then make a circle around it, and then highlight it with a yellow marker and so on, as long as each of them doesn’t carry special meaning, all these ways to distinguish it, make together just what each of them does separately – draw attention to the word.
The second law is originally stated as:
The value of a crossing made again is not the value of the crossing.
One more way to interpret the mark is as an invitation to cross from the inside to the outside. As such it serves as operator and an operand at the same time. The outer mark operates on the inner mark and turns it into void.
If the inner mark turns its inside, which is empty, nothing into outside, which is something, then the outer mark turns its inside, which is something, due to the operation of the inner mark, into nothing.
Picture a house with fence that fully surrounds it. You jump over the fence and then continue walking straight until you reach the fence and then jump on the other side. As long changing your being inside our outside is concerned, crossing twice is equal to not crossing at all.
The whole arithmetic and algebra of George Spencer-Brown is based on these two equations. Here is a summary of the primary algebra.
The third equation has a variable in it.
a = (a)
It has two possible values, mark or void. We can test what happens, trying the two possible values on the right side of the equation.
Let a be void, then:
a = ( )
Thus, if a is void, then it is a mark.
Now, let a be mark, then:
a = (()) = .
If a is a mark, then substituting a with a mark on the right side will bring a mark inside another, which according to the law of crossing will give the unmarked state, the void.
This way we have an expression of self-reference. It can be seen in numerical algebra in equations such as x = 1/x, which doesn’t have a real solution, so it could only have an imaginary one. It can be traced in logic and philosophy with the Liar paradox, statements such as “This statement is false”, or the Russell’s set of all sets that are not members of themselves.
However, in the calculus of indications, this form lives naturally. In a similar way as the distinction creates space, the self-reference, the re-entry, creates time.
There is no magic about it. In fact all software programs not just contain self-referential equations, they can’t do without them. They iterate using expressions such as n = n + 1.
Recrossing
The Laws of Form resonate in religions, philosophies and science.
Chuang Tzu:
The knowledge of the ancients was perfect. How so? At first, they did not yet know there were things. That is the most perfect knowledge; nothing can be added. Next, they knew that there were things, but they did not yet make distinctions between them. Next they made distinctions, but they did not yet pass judgements on them. But when the judgements were passed, the Whole was destroyed. With the destruction of the Whole, individual bias arose.
The Tanakh (aka Old Testament ) starts with:
In the beginning when God created the heavens and the earth, the earth was a formless void… Then God said, ‘Let there be light’; and there was light. …God separated the light from the darkness. God called the light Day, and the darkness he called Night.
That’s how God made the first distinction:
(void) light
And then, in Tao Te Ching:
The nameless is the beginning of heaven and earth…
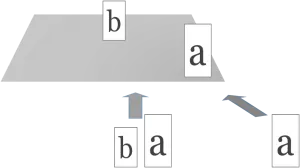
Analogies can be found in Hinduism, Buddhism and Islamic philosophy. For example the latter distinguishes essence (Dhat) from attribute (Sifat), which are neither identical nor separate. Speaking of Islam, the occultation prompts another association. According to the Shia Islam, the Twelfth imam has been living in a temporary occultation, and is about to reappear one day. Occultation is also one of the identities in the primary algebra:
In it the variable b disappears from left to right, and appears from right to left. This can be pictured by changing the position of an observer to the right, until b is fully hidden behind a, and then when moving back to the left, b reappears:
Another association, which I find particularly fascinating, is with the ancient Buddhist logical system catuskoti, the four corners. Unlike the Aristotelian logic, which has the principle of non-contradiction, and the excluded middle, in catuskoti there are four possible values:
not being
being
both being and not being
neither being or not being
I find the first three corresponding with the void, distinction, and re-entry, respectively, which is in line with Varela’s view that apart form the unmarked and the marked state, there should be a third one, which he calls the autonomous state.
The fourth value would represent anything which is unknown. If we set being as “true”, and not-being as “false”, then every statement about the future is neither true nor false at the moment of uttering. And we make a lot of statements about the future, so it is common to have things in the fourth corner.
The fourth value reminds me, and is reminded by the Open World Assumption, which I find very useful in many cases, as I mentioned here, here, and here. It also tempts to add a fourth statement to the initial three:
To not know is not to know there is not.
Catuskoti fits naturally to the Buddhist world-view, while being at odds with the Western one. At least until recently, when some multi-valued logics appeared.
George Spencer-Brown, Louis Kauffman, William Bricken demonstrated that many of the other mathematical and logical theories can be generated using the calculus of indications. For example, in elementary logic and set theory, negation, disjunction, conjunction, and entailment, can be represented respectively with (A), AB, ((A)(B)), and (A)B, so that the classical syllogism ((A entails B) and (B entails C)) entails (A entails C), can be shown with the following form:
If that’s of interest, you can find explanations and many more examples in this paper by Louis Kauffman.
“Laws of Form” inspired extensions and applications in mathematics, second-order cybernetics, biology, cognitive and social sciences. It influenced prominent thinkers like Heinz von Foerster, Humberto Maturana, Francisco Varela, Louis Kauffman, William Bricken, Niklas Luhmann, and Dirk Baecker.
Reentering
Self-reference is awkward: one may find the axioms in the explanation, the brain writing it’s own theory, a cell computing its own computer, the observer in the observed, the snake eating its own tail in a ceaseless generative process.
F. Varela, A Calculus for Self-reference
Is re-entry fundamental or a construct? According to George Spencer-Brown, it’s a construct. Varela, on the other hand, finds it not just fundamental but actually the third value, the autonomous state. He brings some quite convincing arguments. For Kauffman, the re-entry is based on distinction, just as distinction is based on re-entry:
the emergence of the mark itself requires self-reference, for there can be no mark without a distinction and there can be no distinction without indication (Spencer-Brown says there can be no indication without a distinction. This argument says it the other way around.). Indication is itself a distinction, and one sees that the act of distinction is necessarily circular.
That was the reason I presented three statements, and not only the first two, as a summary of the calculus of indications.
Similar kind of reasoning can be applied to sense-making. It can be seen as an interplay between autonomy and adaptivity. The autonomy makes the distinctions possible and the other way round. Making distinctions on distinctions is in fact sense-making but it also changes the way distinctions are made due to adaptivity. At this new level, distinctions become normative. They have value in the sense that the autonomous system has attitude, has re-action determined by (and determining) that value. The simplest and most clearly distinguished attitudes are those of attraction, aversion and neutrality.
This narrative may imply that values are of a higher order. First distinctions are made, then sense, and then values, in a sort of a linear chain. But it is not linear at all.
As George Spencer-Brown points out, a distinction can only be made by an observer, and the observer has motive to make certain distinctions and not others:
If a content is of value, a name can be taken to indicate this value.
Thus the calling of a name can be identified with the value of the content
Thus values enable distinctions and close the circle. Another re-entry. We can experience values due to the significance that our interaction with the world brings forth. This significance is based on making distinctions, and we can make distinctions because they have value for us.
But what is value and is it valuable at all? And if value is of any value, what is it that makes it such?
Ezequiel Di Paolo defines value as:
the extend to which a situation affects the viability of a self-sustaining and precarious network of processes that generates and identity
And then he adds that, the “most intensely analysed such process is autopoiesis”.
In fact the search for a calculus for autopoiesis was what attracted Varela to the mathematics of Laws of Form in the first place. It was a pursuit to explain life and cognition. Autopoiesis was also the main reason for Luhmann and Baecker’s interest but in their case for studying social systems.
The operationally closed networks of processes in general, and the autopoiesis in particular, show both re-entry, and distinction enabled by this re-entry and sustaining it. For the operationally closed system all its processes enable and are enabled by other processes within the system. The autopoietic system is the stronger case, where the components of the processes are not just enabled but actually produced by them.
Both are cases of generating identity, which is making a distinction between the autonomous system and environment. Environment is not everything surrounding it, but only the niche which makes sense to it. This sense-making is not passive and static, it is a process enacted by the system which brings about its niche.
Identity generation makes a distinction which is also what it is not, a unity. That is how living systems get more independent from the environment, which supplies the fuel for their independence and absorbs the exhaust of practising independence. And more independence would mean more fuel, hence bigger dependence. The phenomenon of life is a “needful freedom”, as pointed out by Hans Jonas.
Zooming out, we come back to the observation of George Spencer-Brown:
the world we know is constructed in order to see itself.[…] but in any attempt to see itself, […]it must act so as to make itself distinct from, and therefore false to, itself.
Closing the circle from distinctions to sense-making through value-making to (new) distinctions, solves the previous implication of linearity but it may now be misunderstood to imply causality. First, my intention was to point them out as enabling conditions, not treating for now the question if they are necessary and sufficient. Second, the circle is enabled by and enables many others, the operationally closed self-generation of identity being of central interest so far. And third, singling out these three operations is a matter of distinctions, made by me, as an act of sense-making, and on the basis of certain values.